La démonstration et les mathématiques



Notions également traitées dans ce chapitre : La raison et le réel - La vérité - Théorie et expérience

Une image, un texte



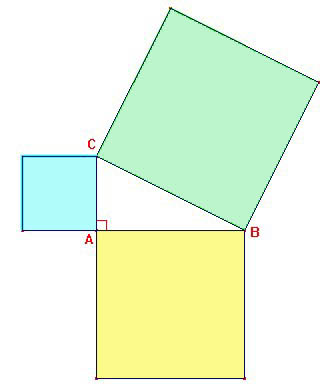
Théorème de Pythagore

"Ces longues chaînes de raisons, toutes simples et faciles, dont les géomètres ont coutume de se servir pour parvenir à leurs plus difficiles démonstrations, m'avaient donné occasion de m'imaginer que toutes les choses, qui peuvent tomber sous la connaissance des hommes, s'entre-suivent en même façon, et que, pourvu seulement qu'on s'abstienne d'en recevoir aucune pour vraie qui ne le soit, et qu'on garde toujours l'ordre qu'il faut pour les déduire les unes des autres, il n'y en peut avoir de si éloignées auxquelles enfin on ne parvienne, ni de si cachées qu'on ne découvre. Et je ne fus pas beaucoup en peine de chercher par lesquelles il était besoin de commencer : car je savais déjà que c'était par les plus simples et les plus aisées à connaître ; et considérant qu'entre tous ceux qui ont ci-devant recherché la vérité dans les sciences, il n'y a eu que les seuls mathématiciens qui ont pu trouver quelques démonstrations, c'est-à-dire quelques raisons certaines et évidentes, je ne doutais point que ce ne fût par les mêmes qu'ils ont examinées ; bien que je n'en espérasse aucune autre utilité, sinon qu'elles accoutumeraient mon esprit à se repaître de vérités et ne se point contenter de fausses raisons."


Descartes, Discours de la méthode, 1637.


Problèmes essentiels

  1. Qu'est-ce que démontrer ? Dans quels domaines parle-t-on de démonstrations ? Ne démontre-t-on qu'en mathématiques ? En quoi la démonstration est-elle un mode particulier d'accès à des vérités, des connaissances ou des certitudes ?

  2. Quelle forme de certitude la démonstration mathématique nous permet-elle d'atteindre ? Ou, autrement dit, qu'est-ce qu'une "vérité mathématique" ? Le mot "vérité" a-t-il ici le même sens que lorsqu'il est utilisé dans la vie courante ou dans les sciences (aussi bien les sciences de la nature que les sciences humaines) ?

  3. La question des limites de la démonstration : Toutes les vérités peuvent-elles être acquises par la démonstration ? Quels sont les autres moyens d'accès à la vérité ?

Cours

  1. Qu'est-ce qu'une démonstration ?


  2. Les mathématiques, modèle de toute connaissance ?

    3. Pour quelles raisons peut-on concevoir les mathématiques ou la logique comme un modèle pour les autres connaissances ? Qu'est-ce qui fait leur force ? Quelles sont les limites de ce modèle ?

    1. De Platon à Leibniz, en passant par Descartes, nombreux ont été les philosophes qui ont, tout au long de l'histoire de la philosophie, considéré les mathématiques, et le type de raisonnement qu'elles mettent en oeuvre, comme un modèle, dont les autres domaines du savoir, y compris la philosophie, devrait s'inspirer.
        Ainsi raconte-t-on, que Platon avait fait inscrire au fronton de son école que "Nul n'entre ici s'il n'est géomètre" (i.e mathématicien) : pour lui, les mathématiques ont cette vertu d'apprendre aux hommes que le vrai ne s'atteint pas par les sens (le monde sensible), mais par la raison (le monde des idées. Elles nous accoutument à tourner notre âme vers les Idées, à nous libérer des illusions de la caverne : cf. allégorie du même nom, dans La République (et dans le chapitre sur La vérité).
        Ce statut de modèle des mathématiques et des démonstrations qu'elles déploient, est particulièrement visible dans ce texte de Descartes mis en introduction de la fiche et tiré du Discours de la méthode.
        Voir également cet extrait du livre L'axiomatique du philosophe et logicien Robert Blanché dans lequel il explique pourquoi les Eléments d'Euclide ont longtemps fasciné les esprits soucieux d'ordonner les pensées et de construire l'édifice de la connaissance de manière solide et systématique : les mathématiques telles qu'elles ont été axiomatisées par Euclide sont un modèle de "théorie déductive".

    2. Kant, au XVIIIe siècle, salue lui aussi les progrès que les mathématiques et la logique ont connu depuis bien plus longtemps que les autres sciences, mais il remarque qu'ils sont dûs au caractère particulier de leurs objets (les mathématiciens travaillent sur des objets idéels, des concepts, qu'ils ont qui plus est créés), alors que dans les autres sciences (non strictement formelles), l'esprit à affaire à autre chose qu'à lui-même : le physicien ou le biologiste étudient des réalités naturelles, qui exsitent indépendamment de l'esprit humain, et que celui-ci cherche à connaître, on pourrait presque dire, "à rejoindre"...
        Lire ces deux textes :
      - La logique comparée aux autres sciences
      - Démonstration mathématique et connaissance philosophique.

  3. Qu'est-ce qu'une vérité mathématique ?

    4.   Lorque l'on parle de la vérité d'une proposition (d'un théorème ou d'une propriété par exemple) en mathématiques, le mot "vérité" a-t-il le même sens que lorsque l'on parle de la vérité d'un énoncé dans les sciences de la nature (physique ou biologie) ou même dans les sciences humaines (histoire, sociologie etc.) ?
      Nous avons vu dans le chapitre sur la vérité que l'on devait distinguer deux grands types de vérités : les vérités de fait et les vérités de raison (cf. en particulier le texte de Hume) : les propositions "L'eau bout à 100°" et "Napoléon est mort à Saint Hélène", d'une part, et "La somme des angles d'un triangle est égale à 180°", ne sont pas de même nature : pour rappel, une vérité de fait énonce une conformité ou une correspondance entre ce que je dis et ce qui est (la phrase "il pleut" est vraie si effectivement il pleut au moment où je le dis, là où je le dis); la "vérité" de l'affirmation "par un point extérieur à une droite donnée on ne peut mener qu'une parallèle à cette droite" n'a de sens que dans le système constitué par la géométrie euclidienne. Elle ne désigne "que" la cohérence de cet énoncé avec les autres éléments du système. On parle alors non pas de "vérité-correspondance", mais de "vérité-cohérence".

    1. Ainsi, comme le remarque dans ce texte Robert Blanché, il faut distinguer "vérité" et "validité" d'un énoncé.

    2. Enseignement de l'invention des géométries non-euclidiennes :
        Que les vérités mathématiques se distinguent des vérités au sens commun du terme a été encore rendu davantage évident à l'occasion de la découverte (ou de l'invention!) des géométries dites non-euclidiennes au XIXe siècle, ainsi que nous l'explique ici (encore!) Robert Blanché :
      - Les géométries non-euclidiennes et la vérité mathématique (Questions sur ce texte).

        La conclusion de tout cela est, pour Henri Poincaré, que Les axiomes sont des conventions.

        Le mathématicien, logicien et philosophe Bertrand Russell va même plus loin, avec un certain humour, en disant que "la mathématique peut être définie comme le domaine dans lequel nous ne savons pas de quoi nous parlons, ni si ce que nous disons est vrai" ! Paradoxal retournement pour cette discipline qui devait servir de modèle de certitude à toutes les autres !...
      - Bertrand Russell, Mathématiques et vérité.

  4. Peut-on tout démontrer ?

      5.   Jusqu'où s'étend le pouvoir de la démonstration ? Permet-elle d'atteindre des certitudes absolues ? Ces deux questions soulève le problème des limites de la démonstration. On peut mettre en évidence des limites internes, propres à toute démonstration (ce qui veut dire qu'il faut renoncer à l'idée d'une démonstration qui serait parfaite : cf. premier point ci-dessous); mais aussi des limites externes, c'est-à-dire montrer que toutes les vérités ne sont pas susceptibles d'être atteinte par la voie de la démonstration (cf. Point 2).

    1. Limites internes à toute démonstration :
      - Pascal, De l'esprit géométrique : qu'il est impossible de tout démontrer.

    2. Limites externes (ou les vérités qui échappent à la démonstration) :
         Toutes les vérités ne sont pas susceptibles d'être démontrées, au sens fort du mot démonstration. Elles ne sont pas toutes établies seulement par des raisonnements logiques ou mathématiques.
         Dans la vie courante, comme dans les sciences expérimentales, les énoncés portent sur des faits extérieurs à l'esprit (qu'il s'agisse de la psychologie, de la sociologie, c'est-à-dire des sciences humaines, ou des sciences de la nature, comme la physique ou la biologie). La vérité de ces énoncés ne se démontre donc pas de manière purement spéculative, mais elle se constate ou s'expérimente : pour savoir si lorsque je dis "il neige", je dis vrai, il regarder dehors. Aucun raisonnement purement logique ne peut justifier cette proposition !
         D'autre part, il y a encore d'autres domaines comme l'art ou la philosophie qui entretiennent également un rapport étroit avec la recherche de la vérité, mais dans lesquels on procède par d'autres moyens que la stricte démonstration :
           - Le philosophe pense, émet des hypothèses ou des théories, il les argumente, et cherche à les justifier, à les "démontrer" dans un certain sens, mais elles n'ont jamais ou rarement le même caractère de certitude que les vérités mathématiques. Elles sont toujours révisables ou discutables.
           - L'artiste, quant à lui, poursuit certainement une forme de vérité sur le monde, l'existence, l'homme etc., mais la nature de cette vérité et les moyens d'y accéder sont très différents de la nature des vérités formelles de la logique et des mathématiques, et des procédures qui les établissent. (voir le chapitre sur l'art)

         Références possibles :
      - Il y a des vérités qui sont saisies par l'intuition, le sentiment ou le "cœur" et non par la démonstration ou la déduction :
      Pascal, Vérités de cœur/vérités de raison.
      - La réalité ou l'existence d'une chose ne se démontrent pas, mais s'éprouvent, se constatent. Autrement dit, seule l'expérience peut attester de l'existence d'un objet : Voir ces deux textes de Hume :
         Vérités de raison / vérités de fait.
         La raison et l'expérience.

Ressource externe (pour approfondir)

- Un collègue, Gabriel Gay-Para, a fait un très bon diaporama, qui recoupe beaucoup d'éléments abordés ici, en particulier la question des limites de la démonstration :

Vocabulaire

Distinguer :

Démontrer/prouver : "On prouve par des témoignages, par des actes, par des preuves, en un mot; on démontre par des arguments. Un fait se prouve, mais ne se démontre pas. Une proposition se démontre; mais elle se prouve aussi, quand les arguments sont considérés comme des preuves." (Littré)

Intuition/Déduction : Ces termes désignent deux manières différentes d'accéder au vrai.
  L'intuition est une opération de l'esprit par laquelle il saisit une vérité dans une certaine immédiateté. L'intuition peut être soit intellectuelle, soit sensible.
  La déduction suppose quant à elle la mise en œuvre d'une pensée discursive (voir définition de ce terme dans le lexique), d'un raisonnement, par lequel la vérité d'une proposition va être établie (par étapes successives) en la tirant d'une ou plusieurs propositions antécédentes qui en constituent les prémisses. Voir partie lexique du site.

Axiome/postulat/Théorème : Les deux premiers termes dont les différences sont subtiles et sujettes à discussion désignent des propositions qui servent de fondements à une démonstration en mathématiques et qui sont posées sans être démontrées : soit parce que leur vérité semble évidente par elle-même (et que ces propositions sont considérées comme n'ayant pas besoin d'être démontrées ou comme indémontrables), soit parce qu'est affirmé et assumé leur statut de pures conventions. (Voir également le lexique)
   Un théorème en revanche est une proposition démontrée.

Vérité formelle/vérité matérielle ou vérité de raison/vérité de fait : Les vérités formelles sont celles que l'on obtient à titre de conclusions d'un raisonnement déductif ou d'une démonstration. La raison seule suffit à les établir. Les vérités de fait ou matérielles portent sur des états de fait extérieurs à l'esprit, donc sur une forme d'observation (directe ou indirecte selon le domaine concerné). Une vérité formelle est nécessaire; une vérité de fait a un caractère contingent irréductible.

Exemples de sujets




Dernière mise à jour : 22/02/2019